RGB Classic Games Forum

This topic is analogous to the Distributed Computing Projects, so I thought that I would start
a new thread for this. Although some problems can be solved by computation, but some
problems can only be solved by manually working out and by some theorems, so this is in
no way related to Distributed Computing Projects. However, I hope that this will be an
interesting topic.

In 1900, Hilbert put forward 24 problems in mathematics, all of which were unsolved at that time,
for research in the 20th century, along with some prizes, for the first correct solution. The problems,
as well as the status of these problems can be found out at
http://en.wikipedia.org/wiki/Hilbert%27s_problems

In 2000, the Clay Math Institute, put forth 7 problems, and offers $1000000 prize for the first
correct solution for each of them. They are known as Millennium Prize Problems. The problems
can be found out at
http://www.claymath.org/millennium/

It seems that the Poincare Conjecture has already been resolved in 2003, but I am not sure of it.

See also
http://www.unsolvedproblems.org/UP/index.htm
for other unsolved problems in Mathematics, Logic and Cryptography.

Here are the descriptions of the important unsolved problems in mathematics:

Riemann Hypothesis:
It claims that all the non-trivial zeros of the Zeta Function lie on the critical line with Real Part = 1/2.
If proved, it will have a tremendous impact on Number Theory and many bounds on prime estimates
can be improved and primality proving can be simplified. For the last 140 years, no proof has been
given, and it has been proved that infinitely many zeros lie on the critical line and atleast 40% of
the non-trivial zeros lie on the critical line. The Zeta Grid distributed computing computing project
has verified that the first 1.5 billion zeros lie precisely on the critical line.

P = NP
This is the important unsolved problem in theoretical computer science. It asks whether a deterministic
polynomial time algorithm exists for every problem that can be solved in polynomial time using a
non-deterministic Turing Machine (say a NP-complete problem). If there exists a deterministic
polynomial time algorithm for one NP-complete problem, then P = NP, and a deterministic polynomial
time algorithm exists for all NP-complete problems. Otherwise P ≠ NP, and many interesting problems
will not be practically solvable. NP-complete problems are those whose algorithms can be derived
and are similar to the satisfiability problem, example: Hamiltonian cycle, Traveling salesman problem,
vertex cover problem, maximum clique in a graph, subset sum problem, etc. Since the problem has
been posed, nobody was able to prove that P ≠ NP, nor find a deterministic polynomial time algorithm
for one NP-complete problem. Currently known algorithms for NP-complete problems have exponential
time on deterministic Turing Machines and polynomial time on non-deterministic Turing Machines.

Goldbach's Conjecture
This conjecture has been standing for over 300 years unproved. It claims that every even number ≥ 4
is the sum of two primes. So far it has been proved that every number ≥ 14 is the sum of seven primes.

Odd Perfect Numbers
This is another problem, standing unresolved for the last 300 years. A perfect number is a number whose
sum of all the factors is twice the number. Example: 6, 28, 496, 8128... It can easily be proved that every
even perfect number has the form ((2^p)-1)(2^(p-1)) where (2^p)-1 is prime. The problem is to find
an odd perfect number or prove that none exist. It has been checked that there are no odd perfect
numbers till 300 digits, if one exists, it is a perfect square times an odd power of a single prime, it
is divisible by atleast 8 primes, and has atleast 75 prime factors with atleast 9 of them being distinct,
and a prime divisor greater than 20 digits. Carl Pomerance has proved that there are only finitely many
odd perfect numbers, and given a heuristic argument that none of them exist.
http://oddperfect.org/pomerance.html
It has also been conjectured that there are no odd harmonic numbers, i.e. whose sum of reciprocals
of all its factors is an integer. If this is proved, it also implies that there are no odd perfect numbers.

Four color conjecture
It asks for how many colors are minimum needed to paint a graph in a plane, such that each of the
adjacent regions, which share a common edge are of a different color. It is easy to see that a
minimum of 4 colors are needed, and it is not difficult to prove that a maximum of 5 colors is
sufficient. It has been checked that 4 colors are enough for all graphs with upto 40 regions, but
it has not been proved in general that 4 colors are enough to paint any graph.

Legendre's conjecture
This asks whether there is always a prime between two consecutive squares.

Fermat's Last Theorem
This was the famous unsolved problem standing for over 300 years till Andrew Wiles proved in 1995
that no non-trivial integer solution to the equation (x^n)+(y^n)=(z^n) exists, for all n ≥ 3, using the
method of elliptic curves. Fermat himself proved for n=4, Euler proved for n=3, and Kummer proved it
for all regular primes. It was finally resolved by Andrew Wiles in 1995, using a very cumbersome proof,
indeed. However, an extension of this theorem is still unresolved.

Beal's Conjecture
It claims that no non-trivial integer solution to the equation (x^a)+(y^b)=(z^c) exist, for all a, b, c ≥ 3,
if x, y, z are co-prime.

When x, y, z are not co-prime, there exists counter examples, for example
756^3 + 945^3 = 189^4
This conjecture is claimed when x, y, z are co-prime.

Also, this conjecture claims that all of a, b, c ≥ 3, otherwise there also exist counter examples, such as
17^3 + 2^7 = 71^2

There are other minor unsolved problems too. Here are a few of them.

Mersenne Primes
Are there infinitely many values of p such that (2^p)-1 is prime? Currently 44 such Mersenne Primes are known,
and the largest is (2^32582657)-1.

Fermat Primes
The largest known n such that (2^(2^n))+1 is prime is n=4. For n=5 through n=32, all have been checked to
be composite. The lowest n of unknown status is for n=33. The conjecture asks if there are any more such
primes after n=4.

Twin Prime Conjecture
This asks if there are infinitely many twin primes. It is easy to prove that there are infinitely many primes. It
is known that sum of reciprocals of primes diverges to infinite, while the sum of reciprocals of twin primes
converges to a constant known as the Brun's constant. So far it has been proved that there are infinitely
many p for which p+2 is either prime or a product of two primes.

Is every Mersenne Number with a prime exponent square free?
This lies more in the category of as an open question rather than a conjecture. It asks whether all Mersenne
numbers with prime exponents are square free. It is not difficult to prove that if p^2 divides a Mersenne prime,
then it satisfies the equation 2^(p-1) = 1 (mod p^2). Such primes p are called Wieferich primes. The only known
Wieferich primes below 4 × 10^12 are 1093 and 3511. 1093 does not satisfy the equation 2^[(p-1)/2] = 1 (mod p^2)
and 3511 does not divide any Mersenne number with a prime exponent. So, it is known that all Mersenne
numbers with a prime exponent below 4 × 10^12 are square free.

New Mersenne Conjecture
It has been conjectured that if any of the following two statements hold, then also the third one holds.
(1) p is of the form 2^k±1 or 4^k±3
(2) (2^p)-1 is prime
(3) ((2^p)+1)/3 is prime

Catalan's conjecture
This asks whether if 8 and 9 are the only consecutive powers. This has been proved in 2002 by Preda Mihailescu.

Amicable Numbers
Let s(n) denote the sum of all factors of n except itself. Amicable pairs are two numbers x, y such that s(x)=y and
s(y)=x. For example, 220 and 284, 1184 and 1210, 2620 and 2924, 5020 and 5564, 6232 and 6368, 10744 and 10856,
12285 and 14595, 17496 and 18416... The conjecture asks if there are any amicable pairs with one odd and one even.

Sociable Numbers
Just as amicable numbers are sociable numbers of order 2, for sociable numbers of order 3, x, y, z are such that
s(x)=y, s(y)=z, s(z)=x. It is also called as an aliquot 3 cycle. For example, 14316 forms an aliquot 5 cycle, 12496
forms an aliquot 28 cycle and 1264460 forms an aliquot 4 cycle. Aliquot cycles of the order 6, 8, 9 are also known.
This question asks if there are also any aliquot 3 cycles and aliquot 7 cycles.

Euler's brick problem
It asks if there are integers a, b, c > 0 such that if a²+b², b²+c², c²+a² are all perfect squares, a²+b²+c² is also
a perfect square.

Magic Square of Squares
This asks if there is a 3×3 magic square whose entries are all perfect squares.

Ramanujan's Square Equation
This asks if there are values of n besides 3, 4, 5, 7, 15 such that (2^n)-7 is a perfect square. It has been proved
that there aren't any more.

Another Similar Problem
This asks if there are values of n besides 4, 5, 7 such that n!+1 is a perfect square.

Aliquot Sequences
If you keep on iterating the function s(n), you will get a sequence, this is called the aliquot sequence. The conjecture
asks whether all such sequences terminate in a prime or catch in an aliquot cycle. Clearly, this conjecture can only
be resolved by computation. The sequences which do not end in a prime or an aliquot cycle is called an open end
sequence. The open end sequences below 1000 are 276, 552, 564, 660, 966. There are 81 open end sequences
below 10000 currently.

Collatz Conjecture
I recently came across another sequence, known as the Collatz sequence, similar to the Aliquot sequence. Here let
f(x)=x/2, if x is even and f(x)=3x+1, if x is odd, and keep on iterating f(x). The conjecture claims that all such sequences
terminate in 1 for any given starting value of x. However, unlike the Aliquot sequence in which open end sequences
exist, such as 276, 552, 564, 660, 966... this Collatz Sequence has been checked for all values of x upto 2.88×10^18
and they are all found to terminate in 1. Refer to the Wikipedia for more information. And then one more thing... is that
this sequence is easy to compute. For each iteration in the Aliquot sequence, we need to factor the number completely
before we can go to the next iteration, and that factoring of an 80 digit number needs 10 minutes, 100 digit number
takes 12 hours, and 120 digit number requires 5 days on one core of Athlon at 2.4 GHz.

Where did you get your Ph.D from?

Whew, most of that stuff is way beyond me. Made for some interesting reading on an otherwise dull evening though.

Legalmumbojumbo nuch wrote:Where did you get your Ph.D from?

You making fun of me up? I'm in the fourth year of graduation.
Not even yet got up with my bachelor degree in my university still up to date.
-- __ - _

raman22feb1988 wrote: Is every Mersenne Number with a prime exponent square free?
This lies more in the category of as an open question rather than a conjecture. It asks whether all Mersenne
numbers with prime exponents are square free. It is not difficult to prove that if p^2 divides a Mersenne prime,
then it satisfies the equation 2^(p-1) = 1 (mod p^2). Such primes p are called Wieferich primes.

More about Wieferich primes
From the Fermat's little theorem, we have
If p is prime greater than 2, then 2^(p-1) = 1 (mod p).
Are there primes p for which 2^(p-1) = 1 (mod p²)? Yes. They are called Wieferich primes. However, only two of them are known: 1093 and 3511. The search is exhaustive till 4×10^12.

Significance of Wieferich primes
In 1909, Wieferich proved that if the first case of Fermat's Last Theorem is true for a prime exponent p, then 2^(p-1) = 1 (mod p²). Also as stated above, if a square of a prime divides a Mersenne number with prime exponent, p should be a Wieferich prime.

Recall that if p is a prime greater than 5,
(1) By Fermat's Little Theorem, 2^(p-1) = 1 (mod p)
(2) By Wilson's Theorem, (p-1)!+1 = 0 (mod p)
(3) By Fibonacci Primality Test, u(p-L(p|5)) = 0 (mod p) where L is the Legendre Symbol and u(k) represents the k th Fibonacci number.

Equivalently,
(1) Wieferich primes are primes p for which 2^(p-1) = 1 (mod p²). Only 1093 and 3511 are known below 4×10^12.
(2) Wilson primes are primes p for which (p-1)!+1 = 0 (mod p²). Only 5, 13 and 563 are known below 500 million.
(3) Wall-Sun-Sun primes are primes p for which u(p-L(p|5)) = 0 (mod p²). No values of p are known for this case below 10^14.

Though, it has heuristically been conjectured that there are infinitely many primes of each of these types, only a few of each type are known, although there may be a wide gap between the greatest known prime and the next existing prime in each type.

raman22feb1988 wrote: P = NP
This is the important unsolved problem in theoretical computer science. It asks whether a deterministic
polynomial time algorithm exists for every problem that can be solved in polynomial time using a
non-deterministic Turing Machine (say a NP-complete problem).

PRIMES IS IN P
In August 2002, three IIT Kanpur students Agrawal, Kayal and Saxena presented a paper titled 'PRIMES IS IN P', claiming that they have discovered a deterministic polynomial time algorithm to prove the primality of any given number. P denotes the complexity class (deterministic polynomial time algorithm). This algorithm, called the AKS algorithm, in honour of these three students, states that p is prime if and only if
(x-a)^p = (x^p)-a (mod p)

Significance of the AKS algorithm:
(1) Deterministic, polynomial time algorithm.
(2) Unconditional. Take the Miller's Test. It states that if the extended Riemann hypothesis is true, then if p is a SPRP for all bases 1 < a < 2(ln p)², then p is prime. The AKS algorithm does not depend on any unproved assumptions.
(3) General-purpose. Unlike the Lucas Lehmer Test which can be used only for Mersenne Primes and Pepin's Test for Fermat numbers, the AKS algorithm can be used for any given number.
(4) Proves primality. It is not like Fermat's Little Theorem or SPRP test for which there exists infinitely many pseudoprimes and Carmichael numbers for each base. AKS algorithm proves the primality for any given number.

Now, the search is going on if we have overlooked any similar algorithm for factoring or the discrete logarithm problem. The fastest known algorithm for factoring, Number Field Sieve, has sub-exponential running time.

Shor's algorithm for factoring has polynomial running time on a quantum computer, but unless we design a quantum computer capable of holding (2n-1) qubits for factoring a n bit integer, the algorithm will have exponential running time. The Shor's algorithm was discovered in 1994, and in 2001, a group of workers at IBM factored 15 using a 7-qubit quantum computer. This is the current state of art of factoring by using the Shor's algorithm.

Because of Shor's algorithm, factoring is now in complexity class BQP, i.e. quantum polynomial time algorithm. Also that there are no known polynomial time algorithms for the discrete logarithm problem too.

raman22feb1988 wrote: When x, y, z are not co-prime, there exists counter examples, for example
756^3 + 945^3 = 189^4
This conjecture is claimed when x, y, z are co-prime.

Also, this conjecture claims that all of a, b, c ≥ 3, otherwise there also exist counter examples, such as
17^3 + 2^7 = 71^2

The Fermat's Last Theorem claims that there exist no positive integral solution for (x, y, z) for the equation (x^n)+(y^n)=(z^n), when n ≥ 3.

However, when n=2, it becomes the Pythagoreas Equation (x^2)+(y^2)=(z^2).
The solution set to the Pythagoreas Equation is given by
[(u^2-v^2)/2, uv, (u^2+v^2)/2], where u, v are odd, co-prime, and u>v.
This formula gives all the Pythagorean Triplets in the lowest terms.
For example, (3,4,5), (12,5,13), (15,8,17), (20,21,29), etc.

Consider the equation (x^2)+(y^2)=(z^2)+(w^2). This has many solutions, namely, (7,7,1,5), (8,1,4,7), (9,2,6,7), etc.

(x^3)+(y^3)=(z^3) has no solution in positive integers.
But, (10^3)+(9^3)=(12^3)+(1^3) is the famous Ramanujan Equation.
(3^3)+(4^3)+(5^3)=(6^3).

(x^4)+(y^4)=(z^4) has no solution in positive integers.
But, if more variables are allowed, there exist solutions like
(158^4)+(59^4)=(134^4)+(133^4)
(422481^4) = (414560^4)+(217519^4)+(95800^4)

For the higher powers,
(144^5) = (133^5)+(110^5)+(84^5)+(27^5)
(14132^5)+(220^5) = (14068^5)+(6237^5)+(5027^5)

(23^6)+(15^6)+(10^6) = (22^6)+(19^6)+(3^6)

(966^8)+(539^8)+(81^8) = (954^8)+(725^8)+(481^8)+(310^8)+(158^8)
(3113^8)+(2012^8)+(1953^8)+(861^8)=(2823^8)+(2767^8)+(2557^8)+(1128^8)

It has been conjectured that for forming such an equation of degree k, that we need so, atleast k terms.

Chomsky Hierarchy of Languages
Recursively Enumerable > Recursive > Context Sensitive > Context Free

Context Free > Deterministic Context Free > Regular
Context Free > Linear > Regular

Recursively Enumerable
A language for which there exist a Turing Machine that accepts it if the string
is a member of the language, and loops forever without reaching a final state
if the string is not a member of the language.

Recursive
A language for which a Turing Machine halts for every input, in a final state for
valid strings, and rejects the string without entering into a final state for invalid
strings. There should not be any loop without entering into a final state for any
inputs.

If L and L' are both recursively enumerable, then both languages are recursive.
There exist recursively enumerable languages L for which L' is not recursively
enumerable. Not all languages are recursively enumerable and not all recursively
enumerable languages are recursive. If L is recursive, then L' is also recursive,
and subsequently both the languages are recursively enumerable.

Not all languages are recursively enumerable
Let the set of input alphabets be Σ, with N elements. The set of strings generated
by Σ, is a countable set, that is the arithmetic sequence of base N numbers. The
set of languages generated by Σ is the power set of the set of strings, and therefore
not countable. But, the set of all Turing Machines, Q × Γ → Q × Γ × {L, R, S} is
countable. So, not all languages are recursively enumerable.

Turing Machine Halting Problem is undecidable
There is no Turing Machine H which decides if a Turing Machine M will ever halt for any
input that is being provided to it. That is H should halt in a final state "YES" if M halts
for any input that is provided to it, and in a final state "NO" if M does not halt for some
input that is provided to it. There exist no such Turing Machine with this behavior,
and hence the Turing Machine Halting Problem is undecidable.

If the Turing Machine Halting Problem were decidable, every recursively enumerable
language would become recursive, and consequently it is undecidable.

The Hilbert's Tenth Problem
The Hilbert's Tenth Problem asks if there is any algorithm to check if any given Diophantine
equation with integer coefficients has integer solutions. A Diophantine equation is a
polynomial equation with integer coefficients such that its solutions are all considered so
only to be integers. Number of solutions to the Diophantine equation can either be zero,
finite or infinite.

Obviously, the sets of solutions to the Diophantine equation is recursively enumerable.
Sets of solutions can be represented by a vector of N elements for N variables, and
recursively enumerable means countable, that is, there exist a bijective mapping between
the set of natural numbers and this counting function. The sets of solutions are countable
because we can sequentially represent the various sets of solutions, and then count them up,
thus, right in order.

In 1970, Matiyasevich gave a proof that all recursively enumerable sets can be represented
so by a Diophantine equation. That is, the set of recursively enumerable languages and the
Diophantine equation sets are equivalent. Since, not all recursive languages are recursively
enumerable, hence, not all Diophantine sets are recursively enumerable. For recursively
enumerable sets, that are not recursive, there exist no Turing Machine which can decide
whether the given vector is a member of that set. So, for some Diophantine equations,
there exist so no algorithm at all for determining whether the given N-tuple satisfies so
the Diophantine equation that is being given so or not at all so. Thus, the Hilbert's tenth problem is
an undecidable problem, finally.

The proof claims that all the recursively enumerable sets are Diophantine. Thus, the set of
all the exponential functions, prime numbers, factorial, primorial, binomial coefficients, squares,
cubes, Fibonacci, Lucas numbers, everything, satisfy so atleast some of the polynomial equations
that are being given so to be available only so, thus. Indeed, they can be represented so by
some polynomial equation.

Undecidable Problems
1. Turing Machine Halting Problem
2. Unrestricted Grammar is empty set
3. Unrestricted Grammar is finite
4. Modified Post Correspondence Problem
5. Post Correspondence Problem
6. Context Free Language is ambiguous
7. Two Context Free Languages are disjoint
8. The Hilbert's Tenth Problem

If an algorithm for a problem exists with time complexity O(n) on a m-Tape Turing Machine,
then on a standard single tape Turing Machine, there exist an algorithm for the same problem
with time complexity O(n^m).
If an algorithm for a problem exists with time complexity O(n) on a non-deterministic Turing
Machine, then on a deterministic Turing Machine, there exist an algorithm for the same
problem with time complexity O(k^an).

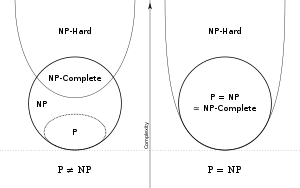
Complexity Classes
P
There exist a deterministic Turing Machine which can solve the problem in polynomial time.
NP
There exist a non-deterministic Turing Machine which can verify the problem in polynomial time.
NP-complete
A problem is NP-complete if
1. It belongs to the complexity class NP
2. Every problem in NP is polynomial time Turing reducible to this problem

NP-complete problems are the hardest of NP problems, and so if we can find a deterministic
polynomial time solution for one NP-complete problem, then all NP problems can be solved
in deterministic polynomial time. Thus, if a deterministic polynomial time solution exists for
one NP-complete problem, then P=NP.
Currently known algorithms for NP-complete problems have polynomial time solution on
non-deterministic Turing Machines and exponential time solution on deterministic Turing Machines.

NP-hard
NP-hard problems are those problems, which are either NP-complete or tougher than that, which
are polynomial time Turing reducible to NP-complete problems. They are indeed, as hard as the
NP-complete problems.

List of NP-complete problems
1. Boolean Satisfiability problem
2. 3-Satisfiability
3. Hamiltonian cycle
4. Travelling salesman problem
5. N-Clique in a graph
6. Vertex covering
7. Independent set
8. Minimum spanning tree
9. Chromatic Number problem (or) Graph Colouring problem
10. Knapsack problem
11. Subset Sum problem
12. Partitioning problem
13. N-puzzle
14. Subgraph isomorphism problem

Hilbert's Tenth Problem:
Devise a process in finite number of steps to decide whether a given Diophantine equation
with integer coefficients has any solution in integers.

Diophantine equation:
A Diophantine equation is a polynomial equation with integer coefficients for which we are
looking for a solution in integers.

Any Linear Diophantine Equation will be of the form ax+by=c, and will have solutions in integers
for x, y if and only if c is a multiple of gcd(a,b). When c=1 and a, b are co-prime then it becomes
the Bezout's equation, and the solutions of x and y are given by the inverses of b (mod a) and
a (mod b) respectively.

For example, Pell's equation has the form x²-ny²=±1. For example, the solutions to x²-2y²=±1 are
given by the convergents of x/y from √2. For example, if we can write √2 in a continued fraction
expansion, 1+1/(2+1/(2+1/(2+...))) then the convergents are given by 1, 1+1/2, 1+1/(2+1/2), and
so on. They are 1/1, 3/2, 7/5, 17/12, 41/29, 99/70, etc.

In fact, if the n th convergent is given by A(n)/B(n) then A(n) satisfies 2A(n-1)+A(n-2) and B(n) satisfies
2B(n-1)+B(n-2).

And the Fermat's Last Theorem is a Diophantine equation. We seek for non-zero integers, with x^n+y^n=z^n,
where n ≥ 3. It has been proved that there is no such solution for any value of n ≥ 3.

Algorithm: Process that terminates in a finite number of steps.

Hilbert's Tenth Problem:
Devise a process according to which it can be determined in a finite number of steps whether the given
Diophantine equation is solvable in rational integers.

Not all problems need to have an algorithm, algorithms exist only for recursive languages, which halt
after accepting or rejecting the input. Recursively enumerable languages on a process, halts
if it accepts the input, or continues forever if the given input is not a member of the language.

Is every Diophantine equation recursive? Clearly, it is recursively enumerable, because we can count
the Diophantine equations, and have a bijective function with the set of natural numbers.

Clearly, the set of odd numbers, even numbers, a random finite set, an infinite set with a regular sequence
of numbers, a random finite set along with an infinite set of regular sequence of numbers are all
can be expressed by using a Diophantine Equation. If a Diophantine Equation D1 = 0 has a set of
integral solutions, and D2 = 0 has another set of integral solutions, then if we want the union of
solutions, then we can put D1.D2 = 0. If we want the intersection of solutions, then we can put
D1² + D2² = 0. Imagine for all the planar points on a circle.

Exponentiation is Diophantine
In 1949, Davis proves that there is a Diophantine set, whose complement is not Diophantine.
Since recursively enumerable sets are not closed under complementation, he speculates that
recursively enumerable sets are isomorphic with the Diophantine equations.

In 1950, Julia Robinson realized the importance of exponentiation for the Hilbert's Tenth problem.
That is she tries to prove that the set of all the powers of 2, 3, etc. can be represented by a
Diophantine equation. If Exponentiation is Diophantine, she realizes that so are the binomial
coefficients, factorial, primorial, primes, squares, cubes, Fibonacci Numbers, Lucas Numbers, etc.

She, unaware of Davis' work tries to prove that the set of triplets a, b, c such that a=b^c is
Diophantine. Failing which, she was lead to a hypothesis, which states that there is a
Diophantine set (a, b) for which
(a, b) is Diophantine implies b<a^a, but for every k>0, there exists a Diophantine set (a, b)
such that b>a^k. This was later called J.R. and by using the properties of Pell's equation,
she proves that J.R. implies that exponentiation is Diophantine.

In 1959, Davis and Putnam starts to study about the Exponential Diophantine sets, and
by using the unproved conjecture that there are arbitrary long arithmetic progressions consisting
of prime numbers, they prove that every recursively enumerable set is Exponential Diophantine,
and J.R. implies that every recursively enumerable set is Diophantine, so Hilbert's Tenth Problem
is undecidable.

In 1960, Robinson realizes to avoid this unproved conjecture in their proof and simplifies the proof.
In the 1960s, Davis and Putnam try to find out various propositions that imply J.R. Matiyasevich
publishes some of the reductions of the Hilbert's Tenth Problem and then Robinson shows that an existence
of infinite Diophantine set of primes would suffice to establish J.R.

In 1970, Matiyasevich establishes 10 simultaneous first and second degree equations which provide a
Diophantine definition for a set of pairs (a, b) such that b is the (2a) th Fibonacci Number.
This proves J.R. and completes the proof that
All recursively enumerable sets are Diophantine.
and so the Hilbert's Tenth Problem is unsolvable.

So, the sets of recursively enumerable languages and the Diophantine Equations are isomorphic.
An algorithm exists only for recursive languages. There exist some recursively enumerable language
that is not recursive, so there exist some Diophantine set that is not recursive. So, there exist
some Diophantine set for which there exist no algorithm to determine whether there exist any integral
solutions. Thus, so we have that the Hilbert's Tenth Problem is undecidable.

Consequences:
So, we have the sets of prime numbers, binomial coefficients, exponentiation, Fibonacci Numbers,
Lucas Numbers, factorial, primorial, squares, cubes, everything to be represented so by using some
Diophantine Equation, at all, thus.

We see towards the negative side of the problem: Undecidability of the problem, so there exist no
general algorithm at all to determine about the problem.

The Turing Machine halting problem is undecidable. Similarly, we have that the Hilbert's Tenth problem
is undecidable, since we have the Diophantine equation sets to be isomorphic to the recursively enumerable sets.

Since, we do have so, a universal Turing Machine that can accept so any algorithm, by solving any
problem, similarly we have a universal Diophantine equation, that contains all the family of the possible
Diophantine sets, at all, within it up.